
The Sine, Cosine and Tangent functions are often applied to real world scenarios.
What is the height of the tree below?

Show Answer
$ tan(16) = \frac \\ tan(16) = \frac \\ \red x = \frac \\ \red x = 48.8 $
At 57" from the base of a building you need to look up at 55° to see the top of a building. What is the height of the building?
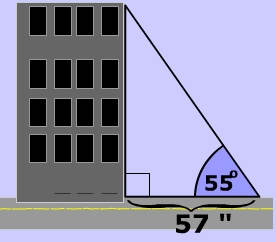
Show Answer
$ tan(55) = \frac \\ tan(55)= \frac < 57>\\ \red x = 57 \cdot tan(55) \\ \red x = 81.4 $
The angle of elevation from a point 43 feet from the base of a tree on level ground to the top of the tree is 30°. What is the height of the tree? Round your answer to the nearest tenth.
First, you should draw and label a picture of this word problem.